|
||
 |
||
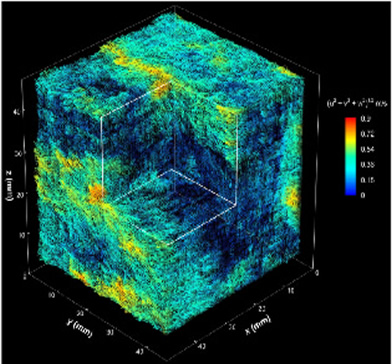
| Instantaneous 3-D velocity distribution of a turbulent flow in a square duct. For clarity, the center-line mean velocity, U = 2.1 m/s, has been subtracted from each vector. The mean flow is along the y direction. The color scales indicate the velocity magnitude. The Reynolds number is ReH=1.2 x 10^5. These data were recorded using Holopgraphic Particle Image Velocimetry systems developed in the Laboratory for Experimental Fluid Dynamics by Prof. J. Katz and co-workers. The experiment and data analysis was carried out within Dr. Bo Tao's PhD research. For details see Tao et al. (2000). |
||
 |
||
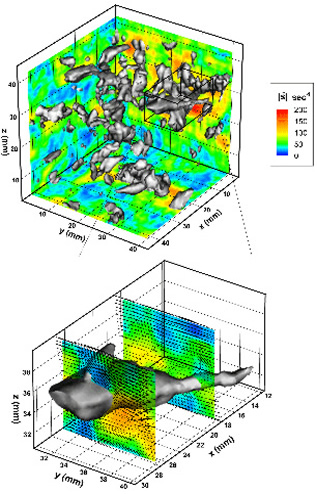
| Iso-vorticity surface of the 3D data in square duct turbulence obtained from the vector field shown above. The color contours are the filtered strain-rate magnitude, at the indicated planes. The enlargement at the bottom shows 2-D cuts of fluctuating velocity distributions around an isolated vorticity iso-surface, superimposed with strain-rate contours. The velocities at the center of the intersections between the planes and the vorticity tube are subtracted from the respective vector maps to reveal the local flow field. For details see Tao et al. (2000). |
||
 |
||
| In collaborations with Prof. M. Parlange, over the past three years a new generation of atmospheric field campaigns have been undertaken. Their goal is to understand the fundamental properties of the subgrid-scale (SGS) motions and transport for large eddy simulation (LES) in atmospheric turbulence. It is well known that especially near the ground, LES is very sensitive to SGS parameterizations and hence it is critical to understand those processes which must be reproduced to faithfully simulate the atmospheric boundary layer (ABL). The field campaigns involved high resolution spatial measurements of velocity and temperature using sonic anemometers mounted in arrays in the atmospheric surface layer.Top: Photograph of array of sonic anemometers during SGS2000 (collaborative field experiment between NCAR and JHU, that took place in Kettleman City, CA, in the summer of 2000). Bottom: schematic of filtering plane using Taylor's hypothesis and averaging over the different sensors. For results from earlier field experiments, see related publications. |
||
 |
||
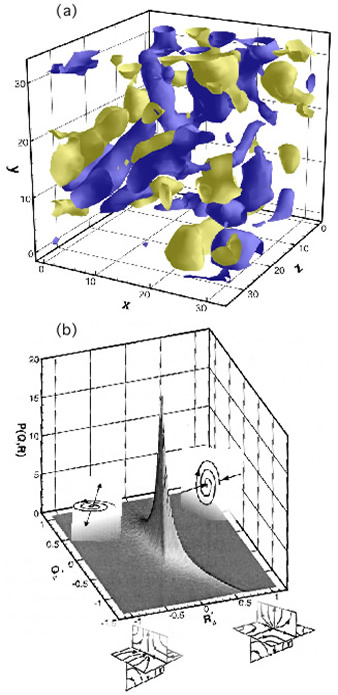
| The figures show newly uncovered properties of relationships between small and large-scale dynamics in turbulence, using data from 3D holographic PIV (obtained and processed in collaboration with Prof. J. Katz -see Tao et al. 2000). Top figure (a) shows iso-surfaces of velocity gradient invariant (QD) measured in square-duct turbulent flow. Invariants are normalized with the mean strain-rate magnitude. Measurements are performed using 3D HPIV (see Tao et al. 2000). The invariant shown is defined as QD = -1/2 AinAni where Aij is the filtered velocity gradient tensor. The values of iso-surfaces shown are QD = - 0.70 (yellow surfaces - indicative of prevalence of strain), and QD = +0.70 (blue surfaces, indicative of vortical regions). The mean flow is along the x-axis. (b) Measured joint-PDF of gradient tensor invariants QD (defined above) and RD defined as RD = -1/3 AinAnkAki. Also indicated are sketches of the local flow structures implied by pairs (RD,QD). This type of analysis is being pursued to quantify the effects of SGS motions on resolved velocity gradient dynamics (van der Bos, Tao, Meneveau & Katz, 2002, Phys. Fluids). |
||
 |
||
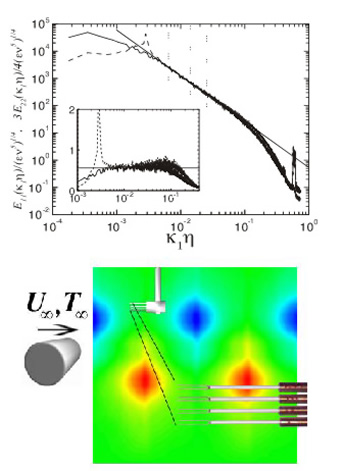
| Hot and cold-wire studies in the heated turbulent wake behind a circular cylinder placed in the Corrsin wind-tunnel performed by postdoctoral scholar Dr. H.S. Kang. The top figure shows extensive inertial range region in both streamwise and cross-stream velocity spectra. The bottom picture is a schematic of the wake and the prove array which allows us to filter the data at various scales in the inertial range (vertical dotted lines in top figure). For more details, see Kang & Meneveau (2001). |
||
 |
||
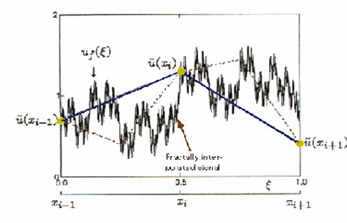
| Different stages during the construction of a fractal signal that 12/13/2013le on a LES mesh xi (solid circles). The solid line shows the first iteration of the mapping, the dotted line shows the second iteration, and the rugged solid line shows the 10th iteration. The number of iterations depends on the viscous cutoff scale. The fractal dimension of the signal shown here is D=5/3 (between 1 and 2, for a smooth or plane-filling object, respectively). We have developed a technique which allows us to compute analytically the subgrid stresses implied by such a fractal signal, without the need to explicitly construct it. This opens the way for a new generation of subgrid models. Applications have been made to forced 1-D Burgers equation (Scotti & Meneveau (1997), and to 3-D forced and decaying Navier-Stokes turbulence, see Scotti and Meneveau (1999). The approach allows us to employ fractals as a predictive tool in the context of coarse-grained, non-linear differential equations. Many open questions and challenges remain to be addressed to further develop this approach. |
||
 |
||
| Isolevel surface of vorticity magnitude in large eddy simulation of a pair of axially colliding vortex rings. The rings approach each other along their axis, stretch, and develop instabilities that subsequently lead to reconnections into ringlets, and to a complicated turbulent flow field. Time advances from left to right, from t G/R2 = 8.8 up to 24.2; the vorticity magnitude of the surface shown is | w|R2 / G= 1.82, where G is the circulation and R is the ring radius. The simulation is based on a 3-D particle vortex method combined with a dynamic eddy-diffusivity model. In the model, the Germano identity is used to evaluate the unknown model coefficient from the resolved field available at discrete particle locations. For more details, see Mansfield et al (1999). |
||
 |
||
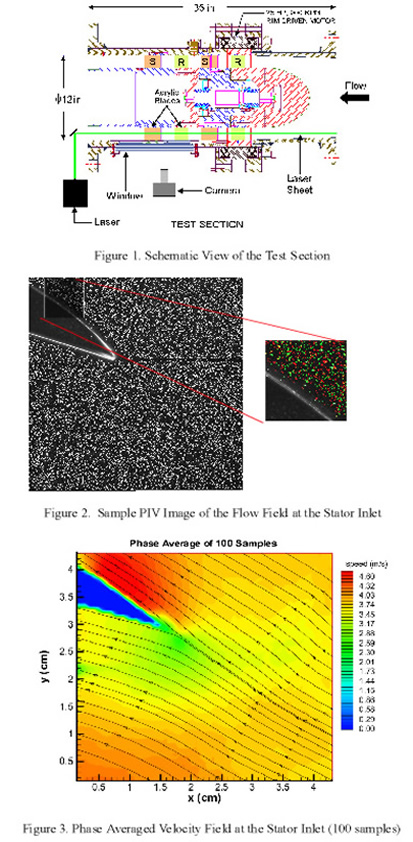
| Performing velocity measurements within complex turbomachinery with multiple blade rows is difficult due to the optical obstruction to the illuminating sheet and to the camera caused by the blades. The new JHU axial turbomachine facility constructed in the Laboratory for Experimental Fluid Dynamics in a collaboration with Prof. J. Katz addresses this problem by using a fluid with the same refractive index as the rotor and stator blades. A schematic description of the setup is presented in Figure 1. The rotor and stator are made of transparent acrylic. Their refractive index is matched with a 62% by weight solution of Sodium Iodide in water. The liquid has a specific gravity of 1.8 and a kinematic viscosity of about 1.08 x 10^-6 m^2/s (depending on temperature, this yields a Reynolds number of 675,000 based on the tip speed and rotor blade chord). This kind of setup allows full optical access to the entire rotor and stator passages without the laser sheet being reflected, blocked or scattered. Vector maps of the instantaneous, phase averaged and passage averaged flow fields are obtained using a 2k x 2k cross-correlation camera. The flow field is seeded with silver coated hollow glas have a mean diameter of 15 solution. Images of streamwise planes are recorded and rms values of velocity fluctuations and turbulent kinetic energy are obtained. Figure 2 is a sample PIV image and an enlarged view showing the double exposures, respectively. The area shown is illuminated after the laser sheet passes through the blade. Phase averaged velocity field generated by averaging 100 instantaneous distributions, all at the same rotor phase, are shown in Figure 3. For related information, see earlier publications on turbomachinery. |
||
|
|
||
|
|
|
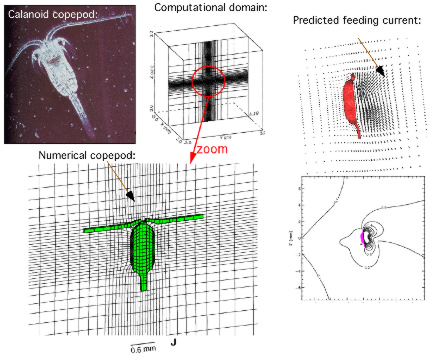
| The basic hydrodynamics of feeding processes of copepods is a crucial element in understanding the global ocean food chain. In work funded by the ONR in collaboration with Prof. T. Osborn, the hydrodynamics of a freely swimming copepod is studied using computational fluid dynamics tools. A typical calanoid copepod geometry is used to generate a numerical copepod geometry by means of body-fitted coordinate system. The copepod's appendage movement causing the feeding currents are approximated using body forces in the flow in the ventral region. The Navier-Stokes equations are solved numerically numerically. The results show that the geometry of the flow field around a freely swimming copepod varies significantly for different behaviors. The results are also used to understand the energetics of different behaviors. For more detailed descriptions of this research, see related list of publications of Jiang et al. |